PERTEMUAN KE- 3
POKOK BAHASAN SISTEM BILANGAN

A. TUJUAN PEMBELAJARAN :
Dengan mempelajari modul ini, secara umum Anda diharapkan mampu untuk memahami sistem bilangan riil. Adapun tujuan pembelajaran yang akan dicapai setelah mempelajari secara khusus Anda diharapkan dapat:
1.1 Mendiskripsikan sistem bilangan riil.
1.2 Menjelaskan jenis-jenis bilangan riil dan kaitannya dengan himpunan untuk bilangan riil tersebut.
1.3 Mencari himpunan penyelesaian suatu pertidaksamaan.
B. URAIAN MATERI
SISTEM BILANGAN
Dalam matematika mumi terdapat pembagian bilangan nyata dan bilangan khayal. Perbedaan utama dari bilangan nyata dan khayal adalah bahwa bilangan nyata mempunyai sifat pembedaan yang jelas antara positif dan negatif sementara bilangan khayal tidak jelas sifatnya, misalnya akar dari suatu bilangan negatif. Dalam matematika ekonomi dan bisnis, hanya bilangan nyata yang digunakan. Skema bilangan bisa digambarkan sebagai berikut :

1. Bilangan Real dan Bilangan Khayal :
• Bilangan Real/nyata rnengandung salah satu sifat yang tegas yaitu dapat
Positif rnaupun Negatif.
Contoh: 2 ; -2 ; 1,2 ; - 1,2
• Bilangan khayal/Imajiner yaitu bilangan yang berupa akar pangkat genap dari suatu bilangan, sehingga tidak jelas sifatnya apakah positif atau negatif.
Contoh:
2. Bilangan Rasional dan Irrasional• Bilangan Rasional adalah hasil bagi antara dua bilangan yang berupa bilangan bulat atau berupa pecahan dengan desimal terbatas atau desimal berulang.
Contoh: 0,1492525 ; 0,149262626
• Bilangan Irasional adalah hasil bagi antara dua bilangan, berupa pecahan dengan desirnal terbatas dan tidak berulang, termasuk bilangan n =3,14... dan e =2,718...
Contoh:
3. Bilangan Bulat dan Bilangan Pecahan • Bilangan Bulat adalah hasil bagi antara dua bilangan yang hasilnya bulat, termasuk 0 (nol). Bilangan bulat dapat dibagi rnenjadi tiga,yaitu:
1) Bilangan bulat positif {1,2,3,4,5,6,7, ... }
2) Nol, bukan positif atau negatif {0}
3) Bilangan bulatnegatif {... , -7,-6,-5,-4,-3,-2,-1}
Bilangan bulat dinotasikan dengan B yang bila diurut kan adalah
B ={... ,-3,-2,-1,0,1,2,3,... }• Bilangan Pecahan adalah hasil bagi antara dua bilangan yang hasilnya pecahan dengan desirnal terbatas atau desirnal berulang.
Selain di atas, masih terdapat beberapa jenis bilangan yang termasuk bilangan bulat, yaitu :
1. Bilangan Asli, yaitu semua bilangan positif tidak termasuk nol. Contoh: A= {1,2,3,4,5, ... }
2. Bilangan Cacah, yaitu semua bilangan bulat positif atau nol. Contoh: C = {0,1,2,3,4,5,6, ... }
3. Bilangan Prima, yaitu bilangan yang habis dibagi oleh bilangan satu dan dirinya sendiri (mempunyai 2 faktor).
Contoh: P = {2,3,5,7,11,13,.. .}
4. Bilangan Komposit, yaitu bilangan yang habis dibagi lebih dari dua faktor.
Contoh: K = {4,6,8, . . .}
SIFAT-SIFAT BILANGAN REAL
1. Trikotomi
Jika x dan y adalah suatu bilangan, maka pasti berlaku salah satu dari x < y atau x > y atau x = y
2. Ketransitifan
Jika x < y dan y < z maka x < z
3. Perkalian
Misalkan z bilangan positif dan x < y maka xz < yz, sedangkan bila z bilangan negatif, maka xz > yz
SIFAT-SIFAT OPERAS! HITUNG BILANGAN BULAT
1. Sifat Komutatif
Sifat komutatif disebut juga sifat pertukaran. Sifat ini hanya berlaku pada operasi penjumlahan dan perkalian.
a. Sifat komutatif pada Penjumlahan
Bentuk umum dari sifat komutatif pada penjumlahan yaitu
a + b = b + a.
Untuk penjelasannya perhatikan contoh berikut ini :
Contoh:
5 + 7 = 12
7 + 5 = 12
Jadi, 5 + 7 = 7 + 5
b. Sifat komutatif pada Perkalian
Bentuk urnurn dari sifat kornutatif pada perkalian yaitu
axb=bxa.
Untuk penjelasannya perhatikan contoh berikut ini : Contoh: 5 x 7 = 35
7 X 5 = 35
Jadi, 5 x 7 = 7 x 5
2. Sifat Asosiatif
Sifat Asosiatif disebut juga sifat pengelornpokan. Sifat ini juga hanya berlaku pada operasi penjurnlahan dan perkalian.
a. Sifat Asosiatif pada Penjumlahan
Bentuk urnurn dari sifat asosiatif pada operasi penjurnlahan
(a + b) + c = a + ( b + c) .
Contoh:
(5 + 3) + 4 = 8 + 4 = 12
5 + (3 + 4) = 5 + 7 = 12
Jadi, (5 + 3) + 4 = 5 + (3 + 4).
b. Sifat Asosiatif Pada Perkalian
Bentuk urnurn dari sifat asosiatif pada operasi perkalian
(axb)xc=ax(bxc).
Contoh:
(5 X 3) X 4 = 15 X 4 = 60
5 X (3 X 4) = 5 X 12 = 60
Jadi, (5 x 3) x 4 = 5 x (3 x 4)
3. Sifat Distributif
Sifat distributif disebut juga sifat penyebaran.
a. Sifat distributif perkalian terhadap penjumlahan
Bentuk urnurn dari sifat distributif penjurnlahan adalah :
ax ( b + c) = (ax b) + (ax c ).
Contoh:
6 X ( 4 + 5 ) = 6 X 9 = 54
( 6 X 4 ) + ( 6 X 5 ) = 24 + 30 = 54
Jadi, 6 x ( 4 + 5 ) = ( 6 x 4 ) + ( 6 x 5 )
b. Sifat distributif perkalian terhadap pengurangan
Bentuk urnurn dari sifat distributif penjurnlahan adalah :
ax(b-c) =(axb)-(axc)
Contoh:
7 X ( 9 - 6) = 7 X 3 = 21
( 7 X 9 ) - ( 7 X 6 ) = 63 - 42 = 21
Jadi, 7 x ( 9 - 6 ) = ( 7 x 9 ) - ( 7 x 6 )
MENGGUNAKAN SIFAT-SIFAT PENGERJAAN HITUNG
Operasi Hitung Perkalian perkalian jika salah satu bilangannya rnerupakan bilangan yang cukup besar, salah satu cara rnernperrnudah pengerjaanya dengan rnenggunakan sifat distriburif.
Contoh:
9 X 456
= 9 X ( 400 + 50 + 6 )
= ( 9 X 400 ) + ( 9 X 50 ) + ( 9 X 6 )
= 3600 + 450 + 54
=4104
OPERAS! TANDA
Untuk (+) = bilangan positif dan (-) = bilangan negatif, berlaku ketentuan :
1. (+) x (+) = (+) atau (+): (+) = (+)
2. (+) x (-) = (-) atau (+) : (-) = (-)
3. (-) x (+) = (-) atau (-) : (+) = (-)
4. (-) x (-) = (+) atau (-): (-) = (+)
5. Jika operasi x/: dan +/- terjadi secara bersarnaan, rnaka dahulukan pengerjaan operasi x/:, barn kernudian operasi +/- dirnulai dari urutan bilangan yang terdepan.
OPERASI PECAHAN
1. Penjumlahan dan Pengurangan Pecahan Murni dan Campuran
Untuk menjumlahkan dan mengurangkan pecahan terlebih dahulu menyamakan penyebutnya. Penyebut yang sama sebaiknya merupakan KPK dari penyebut-penyebut pecahan yang akan dijumlahkan atau dikurangkan. Contoh soal :
Selesaikanlah soal berikut ini!
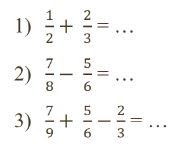
Penyelesaian:

2. Penjumlahan dan Pengurangan Pecahan Desimal
Pecahan desimal dapat dijumlahkan atau dikurangkan dengan cara menyusun ke bawah. Perhatikan bahwa koma desimal hams terletak pada satu garis vertikal.
Contoh soal : Hitunglah!
1) 47,157 + 57,25 + 35,383
2) 2) 375,042 - 99,19 = ...
Penyelesaian:
3. Perkalian Pecahan Murni dan Campuran
Hasil kali pecahan dapat diperoleh dengan cara rnengalikan pernbilang dengan pernbilang dan penyebut dengan penyebut. Jika dalarn perkalian pecahan terdapat pecahan carnpuran, rnaka pecahan carnpuran terlebih dahulu dinyatakan dalarn bentuk pecahan biasa.
Contoh soal :

4. Pembagian Pecahan Murni dan Campuran
Hasil bagi pecahan dapat diperoleh dengan cara rnengalikan dengan kebalikan dari pecahan itu.
Contoh soal :

5. Perkalian Pecahan Desimal
Contoh soal:
1) 6,758 X 10 = .. .
2) 6,758 X 100 = .. .
Penyelesaian:
1) 6,758 X 10 = 67,58
Perhatikan bahwa perkalian dengan 10 dapat dilakukan dengan rnenggeser korna desirnal satu ternpat ke sebelah kanan dari letak sernula.
2) 6,758 X 100 = 675,8
Perkalian dengan 100 dapat dilakukan dengan rnenggeser korna desirnal dua ternpat ke sebelah kanan dari letak sernula.
6. Pembagian Pecahan Desimal
Contoh soal:
1) 268,7: 10 = .. .
2) 268,7: 100 = .. .
Jawab
1) 268,7: 10 = 26,87
Mernbagi dengan 10 dapat dilakukan dengan rnenggeser korna desirnal satu ternpat ke sebelah kiri dari ternpat sernula.
2) 268,7 : 100 = 2,687
Mernbagi dengan 100 dapat dilakukan denga rnenggeser korna desirnal dua ternpat ke sebelah kiri dari ternpat sernula.
C. LATIHAN SOAL/TUGAS
1. Diketahui pasangan bilangan seperti berikut ini!
Tentukanlah:
a. Jurnlah dari pasangan bilangan di atas.
b. Selisih dari pasangan bilangan di atas.
c. Hasil kali dari rnasing-rnasing pasangan.
d. Hitunglah hasil bagi pasangan bilangan di atas.
2. Selesaikanlah perhitungan pecahan bilangan berikut ini!
3. Selesaikanlah perhitungan pecahan desimal berikut ini!
a. 0,32 + 0,09 + 0,13 = .. .
b. 0,32 - 0,09 - 0,13 = .. .
c. 0,32 X 0,09 X 0,13 = ...
d. 0,32 : 0,09 : 0,13 = .. .
Download Modul .pdf
D. DAFTAR PUSTAKA
Badrudin, R. & Algifari. 2003. Matematika Bisnis. Yogyakarta: BPFE
yogyakarta.
Dumairy, 2010. Matematika Terapan untuk Bisnis dan Ekonomi, BPFE, Yogyakarta.
Danang Sunyoto, Matematika Ekonomi, Ardana, Yogyakarta, 2007.
Kalangi, JB. 2005, Matematika Ekonomi dan Bisnis, Jilid 1. Cetakan kelima.
Jakarta: Salemba Empat.
Silaen, S.. 2011, Matematika untuk Bisnis dan Ekonomi, Jakarta: Mitra Wacana Media.
Supranto. J, Matematika untuk Bisnis dan Ekonomi, Universitas Indonesia, Jakarta, 2002.



